Voltage Drop in Consumer Installations According to BS 7671
Editorial StaffSunday, November 29, 2020
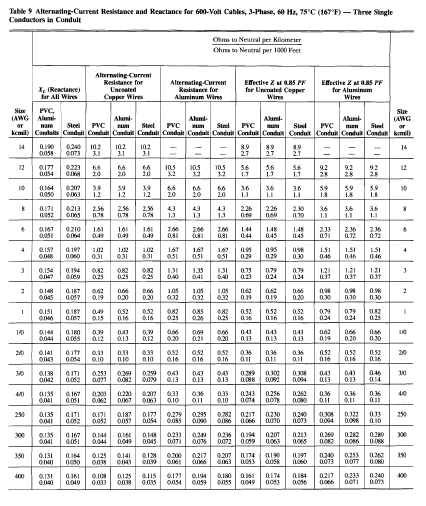
Voltage drop in a consumer’s installation can be a contentious issue. However, it is an important aspect of installation design since if i...
7 Comments
Read





.webp)