Electrical Axis

Green Electronics: Sustainable PCB Manufacturing Practices

Editorial StaffSunday, September 17, 2023

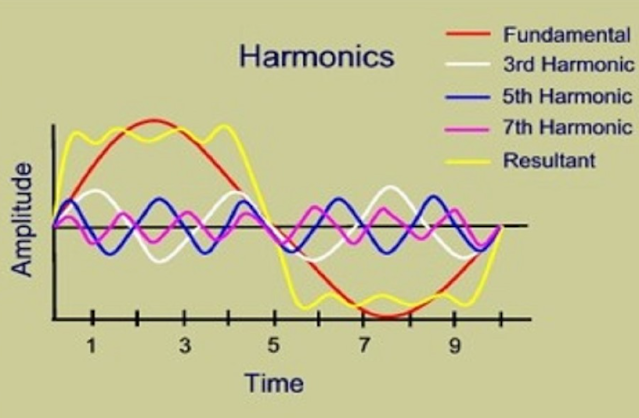
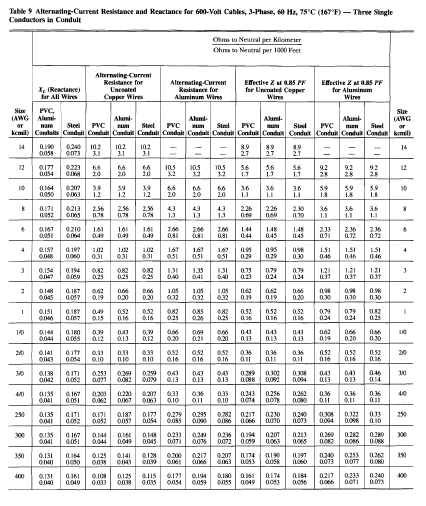
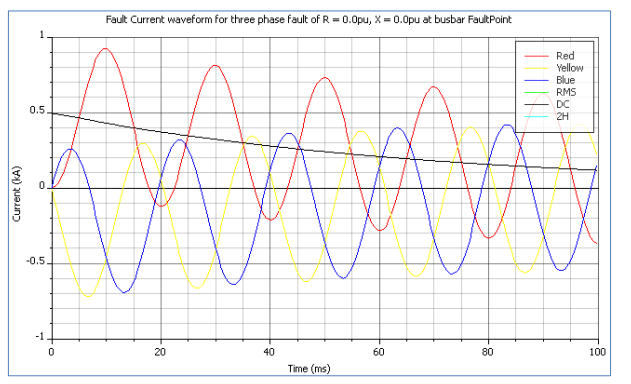
Introduction The electronics business has a significant impact on how our world is shaped at a time when technology and innovation are drivi...

1 Comments

Read

innovation smart grid

Powering the Future: Electric Innovations and Advancements

Editorial StaffWednesday, August 30, 2023

In an era where technological progress is propelling us towards an an increasing number of electrified global, the importance of electric in...

1 Comments

Read

circuit breaker electric protection switchgear

𝗚𝗮𝘀-𝗜𝗻𝘀𝘂𝗹𝗮𝘁𝗲𝗱 𝗦𝘄𝗶𝘁𝗰𝗵𝗴𝗲𝗮𝗿 𝗠𝗼𝗱𝘂𝗹𝗲𝘀 (𝘂𝗽 𝘁𝗼 𝟰𝟮𝟬 𝗸𝗩, 𝟱𝟬 𝗸𝗔, 𝟱𝟬𝟬𝟬 𝗔)

Editorial StaffTuesday, March 28, 2023

Gas Insulated Switchgear | Source: Siemens Energy What is Gas Insulated Switchgear? A Gas Insulated Switchgear (GIS) is a type of switchg...

0 Comments

Read

capacitor electrical harmonics power factor correction

The Influence of Harmonics in Capacitors and Type of Filters for Mitigation

Editorial StaffSaturday, March 25, 2023

What is Harmonics? Harmonics are sinusoidal currents whose frequency is an integral multiple of the fundamental frequency. In simpler terms,...

0 Comments

Read

current transformer electric protection Transformer

What is Current Transformer Knee Point?

Editorial StaffThursday, March 23, 2023

What is Current Transformer? Current transformers (CTs) are devices that are used to measure the current flowing in an electrical circuit. T...

0 Comments

Read

capacitor electrical harmonics power factor correction schneider electric

Power Factor Correction and Harmonic Filtering

Editorial StaffWednesday, March 22, 2023

What is Power Factor? Power factor is a crucial concept in electrical engineering that represents the efficiency of power transfer in an ...

1 Comments

Read

Generator motor starting method

Points to Consider When Sizing Generator Sets for Motor Starting

Editorial StaffSaturday, March 18, 2023

How Motor Starting Affects Generator Sets? Motor starting can have a significant impact on generator sets. When a motor starts, it draws a ...

0 Comments

Read

Subscribe to: Posts ( Atom )

Created By Themexpose

Electrical Axis

Featured Electrical Topics

Recent Posts

Green Electronics: Sustainable PCB Manufacturing Practices

Powering the Future: Electric Innovations and Advancements

𝗚𝗮𝘀-𝗜𝗻𝘀𝘂𝗹𝗮𝘁𝗲𝗱 𝗦𝘄𝗶𝘁𝗰𝗵𝗴𝗲𝗮𝗿 𝗠𝗼𝗱𝘂𝗹𝗲𝘀 (𝘂𝗽 𝘁𝗼 𝟰𝟮𝟬 𝗸𝗩, 𝟱𝟬 𝗸𝗔, 𝟱𝟬𝟬𝟬 𝗔)

The Influence of Harmonics in Capacitors and Type of Filters for Mitigation

What is Current Transformer Knee Point?

Power Factor Correction and Harmonic Filtering

Points to Consider When Sizing Generator Sets for Motor Starting

Follow Us On Facebook

Latest Post

Green Electronics: Sustainable PCB Manufacturing Practices

Popular Topics

Voltage Drop Calculation Based on National Electrical Code

How To Prepare Schedule of Loads

How to Calculate Voltage Drop of Distributed Loads

How to Perform Coordination Study of OCPD and Cable in Electrical Design

What is SELV and PELV Circuits?

How to Calculate Transformer Voltage Drop

What is the Importance of X/R Ratio?

What is Multiple Earthed Neutral?

Motor Circuit Branch Circuit Protection According to NEC 430.52

Powering the Future: Electric Innovations and Advancements

Home Ads