How to Calculate Voltage Drop of Distributed Loads
Voltage drop calculation is necessary in designing electrical system in order to keep our equipment operate normally. Failure to calculate voltage drop properly would result into under-voltage that can damage our equipment.
In other article we discuss about voltage drop calculation based on national electrical code in an ideal way. It is ideal since we are assuming a system of only one load neglecting the possibility that in reality we could encounter a system where load is distributed and the voltage drop is a critical factor.
For example if we are asked to design a lighting of a recreational park where each light is 50 ft apart. Normally we cannot generalized the computation of the voltage drop since it would result into higher cost of conductors.
Example:
Consider figure 1, seven lighting loads each are separated by a distance of 50 ft and carries a load current of 3 amperes. The distance of the source from the first load (Load A) is 20 feet.
a. Determine the size of the conductor that can be used in the given circuit.
b. Perform voltage drop calculation and check if each load has proper voltage level.
Solution:
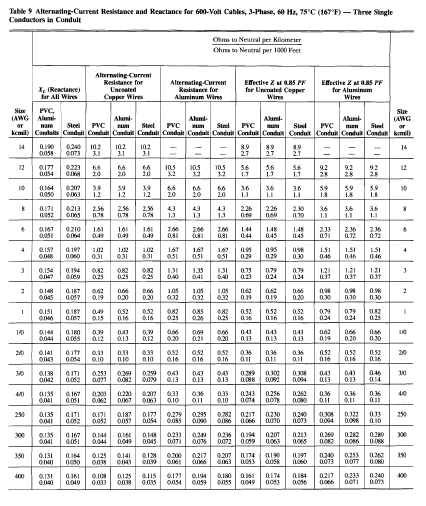
a. By inspection we can say that the total current is the sum of the individual current of each load, thus 3 amperes x 7 loads = 21 amperes. From NEC table 310-16 the right size of conductor to serve 21 amperes is #12 AWG.
b. Perform voltage drop calculation
Point A: From the source to load A
Vd = (2 x 1.7 x 21 x 20 ft) / 1000
Vd = 1.4 Volts
Point B: From load A to load B
Vd = (2 x 1.7 x 18 x 50ft ) / 1000
Vd = 3 volts
Point C: From load B to load C
Vd = (2 x 1.7 x 15 x 50ft ) / 1000
Vd = 2.6 Volts
Point D: From load C to load D
Vd = (2 x 1.7 x 12 x 50ft ) / 1000
Vd = 2 Volts
Point E: load E
Vd = (2 x 1.7 x 3 x 50ft ) / 1000
Vd = 0.51 Volts
Point F: Load D to load E
Vd = (2 x 1.7 x 6 x 50ft ) / 1000
Vd = 1 Volt
Point G: load G
Vd = (2 x 1.7 x 3 x 50ft ) / 1000
Vd = 0.51 Volts
Based on the attained value evaluate each point of the circuit and determine if the voltage level at that point is still suitable to supply its load. Choose 3% allowable voltage drop recommended by the NEC to determine if we need to choose the next higher conductor size or not.
With 3% tolerance the lowest voltage value from 220 V is 213.4 Volts.
Voltage at Point A: 220 V - 1.4V = 218.6 Volts
%Vd @ point A = 1.4V / 220V =0.63% ---> allowed
Voltage at Point B: 220V - 1.4 - 3V = 215.6 Volts
%Vd @ point B = 4.4V / 220V = 2% ---> allowed
Voltage at Point C: 220V - 1.4 - 3V - 2.6V = 213 Volts
%Vd @ point B = 7V / 220V = 3.18% ---> more than 3% is not allowed
therefore lets choose the next higher size of the conductor that will connect load load B to C. In this case lets choose #10 that has Z = 1.1 ohm per 1000 ft.
Recalculating values: Vd at point C = (2 x 1.1 x 15 x 50) / 1000 = 1.65 V
Then it follows that at,
point D = 1.32 V
point E = .33 V
point F = .66 V
point G = .33 V
Thus,
Vd at point C = 220V - 1.4V - 3V - 1.65V = 213.95V
%Vd at point C = 6.05V / 220V = 2.76% ---> allowed
Vd at point D = 213.95 V - 1.32 V = 212.63 V --> not allowed since it is lower than 213.4 Volts at 3% voltage drop tolerance. Discard all succeeding values from point D. Choose next highersize #8 with Z = 0.69
Vd at point D = (2 x 0.69 x 12 x 50) / 1000 = 0.828 Volts
Voltage at point D = 213.95 V - 0.828 V = 213.122 V
% Vd = 6.878/220 = 3.12% ---> more than 3% select next higher, #6 with Z = 0.45
Vd at point D = (2 x 0.45 x 12 x 50) / 1000 = 0.54 Volts
Voltage at point D = 213.95 V - 0.54 V = 213.41 V
% Vd = 6.6V /220V = 3% ---> allowed
At this point we will expect that the next load is above 3% then it is needed to select the next higher conductor size which is #4 with Z = 0.29
Vd at point E = (2 x 0.29 x 3 x 50) / 1000 = 0.087 V
Voltage at point G = 213.41 V - 0.087 V = 213.32 Volts
%Vd = 6.7V / 220V = 3.04% ---> allowed
Vd at point F = (2 x 0.29 x 6 x 50) / 1000 = .174 V
Voltage at point G = 213.32 V - 0.174V = 213.146 V
%Vd = 6.85V / 220V = 3.11% ---> not allowed select next higher size, #3 with Z= 0.23
Recalculation,
Vd at point F = (2 x 0.23 x 6 x 50) / 1000 = 0.138 V
Voltage at point G = 213.41 V - 0.138 V = 213.27 Volts
%Vd = 6.7V / 220V = 3.04% ---> allowed
Vd at point G = (2 x 0.23 x 3 x 50) / 1000 = 0.069 V
Voltage at point G = 213.27 V - 0. 069 V = 213.2 Volts
%Vd = 6.8 V / 220V = 3.11% ---> not allowed select next higher size, #1 with Z = 0.16
Recalculation,
Vd at point G = (2 x 0.16 x 3 x 50) / 1000 = 0.039 V
Voltage at point G = 213.27 V - 0. 069 V = 213.2 Volts
%Vd = 6.7 V / 220V = 3.08% ---> approximately equal to 3% then allow.
Note:
Proper voltage drop calculation has economic rewards. Instead of using uniform large conductors to compensate the voltage losses we can be guided on which portion of the system we can use large sizes and small sizes.
However this is a tedious task especially when we are dealing with systems larger than this example. There are computer software that can help us to make our job easy especially when it comes to repetitive tasks. But before we will seek the assistance of computer for further applications an engineer need to understand first the manual calculation and know how the flow of the computation works.
Click here to access the online voltage drop calculator for street lights.
In other article we discuss about voltage drop calculation based on national electrical code in an ideal way. It is ideal since we are assuming a system of only one load neglecting the possibility that in reality we could encounter a system where load is distributed and the voltage drop is a critical factor.
For example if we are asked to design a lighting of a recreational park where each light is 50 ft apart. Normally we cannot generalized the computation of the voltage drop since it would result into higher cost of conductors.
Example:
Consider figure 1, seven lighting loads each are separated by a distance of 50 ft and carries a load current of 3 amperes. The distance of the source from the first load (Load A) is 20 feet.
a. Determine the size of the conductor that can be used in the given circuit.
b. Perform voltage drop calculation and check if each load has proper voltage level.
 |
| Figure 1. Load Arrangement |
a. By inspection we can say that the total current is the sum of the individual current of each load, thus 3 amperes x 7 loads = 21 amperes. From NEC table 310-16 the right size of conductor to serve 21 amperes is #12 AWG.
b. Perform voltage drop calculation
- by looking at NEC chapter 9 table 8, Z of #12 is 1.7 per 1000 ft.
- From the other article we know that for single phase installations Vd = (2 x Z x I x L) / 1000
Point A: From the source to load A
Vd = (2 x 1.7 x 21 x 20 ft) / 1000
Vd = 1.4 Volts
Point B: From load A to load B
Vd = (2 x 1.7 x 18 x 50ft ) / 1000
Vd = 3 volts
Point C: From load B to load C
Vd = (2 x 1.7 x 15 x 50ft ) / 1000
Vd = 2.6 Volts
Point D: From load C to load D
Vd = (2 x 1.7 x 12 x 50ft ) / 1000
Vd = 2 Volts
Point E: load E
Vd = (2 x 1.7 x 3 x 50ft ) / 1000
Vd = 0.51 Volts
Point F: Load D to load E
Vd = (2 x 1.7 x 6 x 50ft ) / 1000
Vd = 1 Volt
Point G: load G
Vd = (2 x 1.7 x 3 x 50ft ) / 1000
Vd = 0.51 Volts
Based on the attained value evaluate each point of the circuit and determine if the voltage level at that point is still suitable to supply its load. Choose 3% allowable voltage drop recommended by the NEC to determine if we need to choose the next higher conductor size or not.
With 3% tolerance the lowest voltage value from 220 V is 213.4 Volts.
Voltage at Point A: 220 V - 1.4V = 218.6 Volts
%Vd @ point A = 1.4V / 220V =0.63% ---> allowed
Voltage at Point B: 220V - 1.4 - 3V = 215.6 Volts
%Vd @ point B = 4.4V / 220V = 2% ---> allowed
Voltage at Point C: 220V - 1.4 - 3V - 2.6V = 213 Volts
%Vd @ point B = 7V / 220V = 3.18% ---> more than 3% is not allowed
therefore lets choose the next higher size of the conductor that will connect load load B to C. In this case lets choose #10 that has Z = 1.1 ohm per 1000 ft.
Recalculating values: Vd at point C = (2 x 1.1 x 15 x 50) / 1000 = 1.65 V
Then it follows that at,
point D = 1.32 V
point E = .33 V
point F = .66 V
point G = .33 V
Thus,
Vd at point C = 220V - 1.4V - 3V - 1.65V = 213.95V
%Vd at point C = 6.05V / 220V = 2.76% ---> allowed
Vd at point D = 213.95 V - 1.32 V = 212.63 V --> not allowed since it is lower than 213.4 Volts at 3% voltage drop tolerance. Discard all succeeding values from point D. Choose next highersize #8 with Z = 0.69
Vd at point D = (2 x 0.69 x 12 x 50) / 1000 = 0.828 Volts
Voltage at point D = 213.95 V - 0.828 V = 213.122 V
% Vd = 6.878/220 = 3.12% ---> more than 3% select next higher, #6 with Z = 0.45
Vd at point D = (2 x 0.45 x 12 x 50) / 1000 = 0.54 Volts
Voltage at point D = 213.95 V - 0.54 V = 213.41 V
% Vd = 6.6V /220V = 3% ---> allowed
At this point we will expect that the next load is above 3% then it is needed to select the next higher conductor size which is #4 with Z = 0.29
Vd at point E = (2 x 0.29 x 3 x 50) / 1000 = 0.087 V
Voltage at point G = 213.41 V - 0.087 V = 213.32 Volts
%Vd = 6.7V / 220V = 3.04% ---> allowed
Vd at point F = (2 x 0.29 x 6 x 50) / 1000 = .174 V
Voltage at point G = 213.32 V - 0.174V = 213.146 V
%Vd = 6.85V / 220V = 3.11% ---> not allowed select next higher size, #3 with Z= 0.23
Recalculation,
Vd at point F = (2 x 0.23 x 6 x 50) / 1000 = 0.138 V
Voltage at point G = 213.41 V - 0.138 V = 213.27 Volts
%Vd = 6.7V / 220V = 3.04% ---> allowed
Vd at point G = (2 x 0.23 x 3 x 50) / 1000 = 0.069 V
Voltage at point G = 213.27 V - 0. 069 V = 213.2 Volts
%Vd = 6.8 V / 220V = 3.11% ---> not allowed select next higher size, #1 with Z = 0.16
Recalculation,
Vd at point G = (2 x 0.16 x 3 x 50) / 1000 = 0.039 V
Voltage at point G = 213.27 V - 0. 069 V = 213.2 Volts
%Vd = 6.7 V / 220V = 3.08% ---> approximately equal to 3% then allow.
Note:
The calculation above was made for the sake of discussion and demonstration on how the manual voltage drop calculation works. According to the National Electrical Code 3% is just a recommendation and it is not enforceable. Therefore to allow or not to allow the conductor sizes based on the deviation of the voltage drop is still on the discretion of the engineer.Conclusion:
Proper voltage drop calculation has economic rewards. Instead of using uniform large conductors to compensate the voltage losses we can be guided on which portion of the system we can use large sizes and small sizes.
However this is a tedious task especially when we are dealing with systems larger than this example. There are computer software that can help us to make our job easy especially when it comes to repetitive tasks. But before we will seek the assistance of computer for further applications an engineer need to understand first the manual calculation and know how the flow of the computation works.
Click here to access the online voltage drop calculator for street lights.

.webp)