How to Solve Short Circuit Using Point to Point Method
Introduction
Point to point method of short circuit calculation is one of the basic method in finding the short circuit current. Before an engineer use a computer software to determine short circuit current it is recommended that he needs to understand the basic principle and know how to do the manual calculation.
Before we begin the short circuit analysis let us first familiarize the important formula, viz:
1. Short Circuit Current at the terminal of transformer.
- Ixfr-1p = S / VLL , Full load ampere rating of single phase transformer
- Ixfr-3p = S / (1.73 x VLL) , Full load ampere rating of three phase transformer
- Ixfr-sc = Ixfr / % Z
- Ixfr = Current rating of transformer (1p for single phase and 3p for three phase)
- Ixfr-sc = short circuit current of transformer at the terminals
- % Z = percent impedance of the transformer
2. f - factor (the impedance of the cable or busbar between two points where the fault is calculated)
- f = 2 x L x Isc-x / ( C x n x VLL) , for single phase installation
- f = 1.73 x L x Isc-x / ( C x n x VLL), for three phase installation
- f = f - factor
- L = length of the conductor relative to the immediate upstream fault point.
- Isc-x = fault current at any point in the circuit.
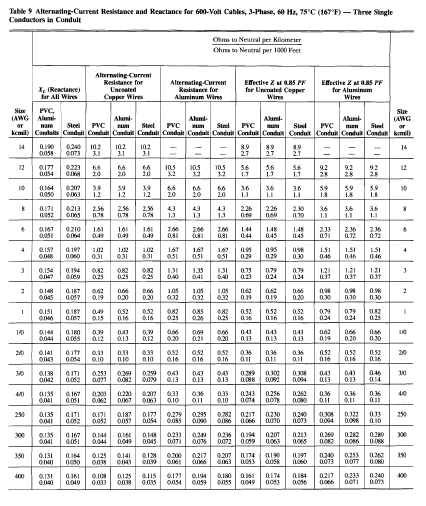
- C = conductor factor and the values are given in the table below.
- n = number of parallel run of conductor.
- VLL = Line to line voltage
3. M- factor (Multiplier to be used against the value of the fault current in the immediate fault point)
- M = 1/ (1 +f )
Consider This System
Now we will perform the point to point short circuit calculation based on the diagram below.
 |
| Figure 1. Typical Load Arrangement |
Calculation of Fault Currents
Fault at Point 1:
The short circuit that can be calculated at this point is coming from the transformer alone. The fault current that we can get is a symmetrical 3 phase fault current. Imagine we will bolt the three terminals of the secondary terminals altogether.
- Ixfr = 500 kVA / (1.73 x 480 ) = 602.11 Amperes
- Isc-1 = Ixfr / % Z
Isc-1 = 602.11 / (.04 x 0.9) = 16. 7 kA
- The 0.9 exist in the equation since the transformer has +/- 10% tolerance and we take the negative value so that we can take the maximum fault current. Take note that the lesser the impedance the higher the fault current.
- If the tolerance is +/- 5% then the factor that will appear in our equation will be 0.95.
Fault at Point 2:
Point 2 has 400 ft. length conductor with 2 conductor per phase. We can apply formula number 3 and 4 at this point, thus:
f = 1.73 x L x Isc-x / ( C x n x VLL), for three phase installation
In this case we can use conductor factor C = 22, 965 based on the following data
- the conductor size is 600 kcmil
- Operating at 480 V which is under 600 V category
- EMT which is a kind of a steel conduit
- The conductor is made of copper
 |
| Table 1. Table of Conductor Factor in Short Circuit Calculation |
Therefore,
- f = (1.73 x 400ft x 16.7 kA) / (22, 965 x 2 x 480) = 0.524
- M = 1 + (1 + f ) = 1 / 1.524 = 0.66
- Isc-2 = M x Isc-1 = 0.66 x 16.7 kA
Isc-2 = 11 kA
Fault at Point 3:
Again we will use the same process and refer to the table given above for the value of conductor factor C.
- f = (1.73 x 500 ft. x 11 kA) / (16, 673 x 1 x 480) = 0.476
- M = 1 / 1.476
- Isc-3 = M x Isc-2 = 0.68 x 11 kA
Isc-3 = 7.48 kA
Fault Point 4:
In fault point 4 we can use the same process but we need to add the locked rotor current (LRA)of the motor during fault condition.
Why we need to add the motor LRA?
- During fault condition the motor whether it is synchronous or induction motor, it will contribute electric current to the fault point.
- During fault condition the supply voltage of the motor will be tend to approach the value of zero and since the rotor still have the effect of inertia (will not stop abruptly), thus it will continue to rotate momentarily right after the fault happen.
- The momentary rotation together with the induced voltage developed in the rotor just before the fault happened will transform the motor into a generator.
- In case of induction motors this scenario will continue until the magnetic flux in the rotor disappear since there is no permanent supply voltage in the rotor of the induction motor.
- Worst case in part of the synchronous motor since the rotor has separate and steady supply, thus the effect of the "motor to generator" transformation will take longer until the rotor stop rotating.
- The value of the current that the motor can contribute during fault condition is equal to the locked rotor current LRA of that motor which is equal to 400% to 600% of the full load amperes of that motor.
In this case the motor is rated 20 HP, operating at 480 Volts, thus:
- FLA = (20 HP x 746) / (1.73 x 480 x 0.85 x 0.8) = 26 Amperes
- LRA = 26 x 600% = 158 Amperes
- The value of LRA is the contribution of the motor to the fault current during fault condition.
- The effect of LRA during fault condition based on the rating of the motor, thus we can say that large motors have significant effect on the system during fault condition.
- f = (1.73 x 200 x 11 kA) / ( 20, 867 x 1 x 480) = 0.38
- M = 1 / 1.38 = 0.72
- Isc-4 = (M x Isc-2) + LRA = (0.72 x 11 kA) + 158 = 8, 078 Amperes or 8.1 kA
Isc-4 = 8.1 kA
Summary of Results:
- Short Circuit Current at Point 1 = 16.7 kA
- Short Circuit Current at Point 2 = 11 kA
- Short Circuit Current at Point 3 = 7.48 kA
- Short Circuit Current at Point 4 = 8.41 kA
What if the fault happened is not a symmetrical three phase fault (Phase to Phase to Phase fault)? We can consider the following rule of the thumb to compute the following faults:
- Phase to Phase (two lines are connected) = use 87% x 3 ph. symmetrical fault current.
- Phase to ground (one line and ground are connected) = 25% x 3 ph. symmetrical fault current.
Phase to Phase Fault Current Values:
- Short Circuit Current at Point 1 = 16.7 kA x 87% = 14.5 kA
- Short Circuit Current at Point 2 = 11 kA x 87% = 9.57 kA
- Short Circuit Current at Point 3 = 7.48 kA x 87% = 6.5 kA
- Short Circuit Current at Point 4 = 8.41 kA x 87% = 7.3 kA
Phase to Ground Fault Current Values:
- Short Circuit Current at Point 1 = 16.7 kA x 25% = 4.1 kA
- Short Circuit Current at Point 2 = 11 kA x 25% = 2.75 kA
- Short Circuit Current at Point 3 = 7.48 kA x 25% = 1.9 kA
- Short Circuit Current at Point 4 = 8.41 kA x 25% = 2.1 kA
References:
- Schneider Electric Cahier no. 158
- General Electric
- Cooper Busman


.webp)









This comment has been removed by a blog administrator.
ReplyDeleteI am appreciative of this blog's ability to provide information for test tag brisbane on such an important subject. I discovered other segments here, and I'm excited to put these new instructions to use.
ReplyDeleteVery Informative. Thanks for sharing the post. Keep Posting. Enroll for IES Online Coaching for more information by exerts
ReplyDeleteThe elastic covering is really a protecting layer that keeps the electricity caught inside. высоковольтный керамический конденсатор
ReplyDelete