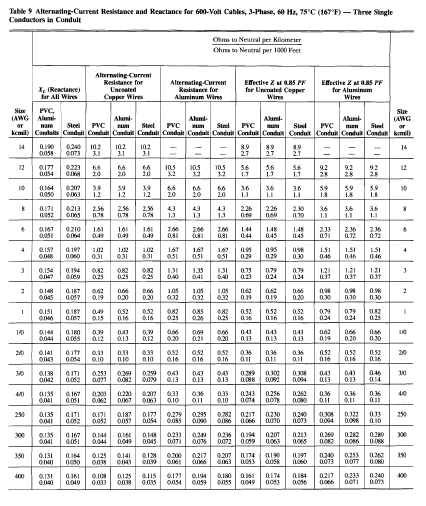
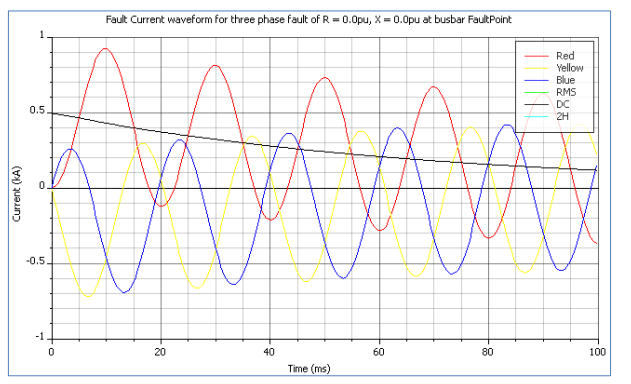
Example: Line to Line Fault Calculation
Editorial StaffSaturday, October 05, 2019
The Line-to-Line fault on a transmission line happens when two current carrying conductors in a three phase system accidentally comes i...
0 Comments
Read



.webp)