Example: Line to Line Fault Calculation

Read

The Line-to-Line fault on a transmission line happens when two current carrying conductors in a three phase system accidentally comes in contact with each other. For this reason, the protective devices of a power system needs to be accurately responsive to avoid severe damage in the system.

See Unbalanced Fault Analysis: Line to Line Fault

For this reason, it is very important to know the procedure of line to line fault calculation in an unbalanced system.

Related articles:



Example: 

From the figure given below, assume that the generator is solidly grounded and neglect the fault impedance. Determine the phase currents and phase voltage when Line to Line fault occurs in the system.



Solution:

From the article Unbalanced Fault Analysis: Line to Line Fault, we know that the positive and negative sequence network is connected in parallel and the zero sequence network is not involved in this type of fault.

From the article Unbalanced Fault Analysis: Line to Line Fault, we know that the equivalent positive sequence network is,

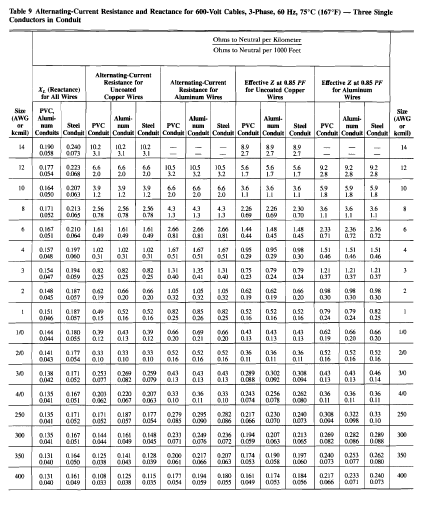
Positive Sequence Network
While the negative sequence network is, 

Negative Sequence Network
Connecting this networks in parallel and getting the Thevenin's equivalent looking at the faulted bus and the reference bus, we can get an equivalent impedance of j 0.25 // j 0.1. 

Thus, the equivalent sequence network can be simplified as one source of 1 (angle 0) per unit and an equivalent impedance of j 0.71 per unit. 

Thus, the positive sequence current will be, 

If-1 = 1 (angle 0)/ j 0.71 = -j 1.41 or 1.41 (angle -90) per unit

Since If-1 = (-If-2), we can directly conclude that the negative sequence current is, 

If-2 = 1.41 (angle 90) per unit --> See Unbalanced Fault Analysis: Line to Line Fault

Therefore we can summarize the sequence components as follows, 
  • If-1 = 1.41 (angle -90) per unit (positive sequence current)
  • If-2 = 1.41 (angle 90) per unit (negative sequence current)
  • If-0 = 0 (zero sequence network is not involved in Line to Line fault)
By using sequence to phase matrix formula, we can get the values of fault current as, 
  • Fault current at phase A = 0.
  • Fault current at phase B = 2.442 (angle 180) pu
  • Fault current at phase C = 2.442 (angle 0) pu
Consider base values, 

Choose: Sb = 20 MVA and kVb = 13.8 kV

then,
Ea = 20 MVA/ 20 MVA = 1 (angle 0) per unit.
Ibase = 20 MVA / (1.73 x 13.8 kV)
Ibase = 0.837 kA

Therefore the actual values of fault currents are, 
  • Fault current at phase A = 0.
  • Fault current at phase B = 2.04 kA (angle 180)
  • Fault current at phase C = 2.04 kA (angle 0) 
Voltage values,
Analyzing positive sequence network equivalent, 
Vf-1 = 1 (angle 0) - (If-1) * (Z1) = 1 - (-j 1.41) (j 0.25) = 0.6475 (angle 0) (+ sequence voltage)

since Vf-1 = Vf-2; therefore Vf-2 = 0.6475 (angle 0) (neg. sequence voltage) See Unbalanced Fault Analysis: Line to Line Fault

Applying the formula of sequence to phase values matrix we can get: 
  • Voltage at phase A = 1.295 (angle 0) pu
  • Voltage at phase B = 0.647 (angle 180) pu
  • Voltage at phase C = 0.647 (angle 180) pu
Applying base values, 

Vbase = 13.8 kV/ 1.73 

Therefore the actual voltage values are, 
  • Voltage at phase A = 10.31 kV (angle 0)
  • Voltage at phase B = 5.15 kV (angle 180)
  • Voltage at phase C = 5.15 kV(angle 180)

For more details See Unbalanced Fault Analysis: Line to Line Fault

power system analysis, fault calculation, unbalance fault, short circuit analysis
Tags :
Created By Themexpose