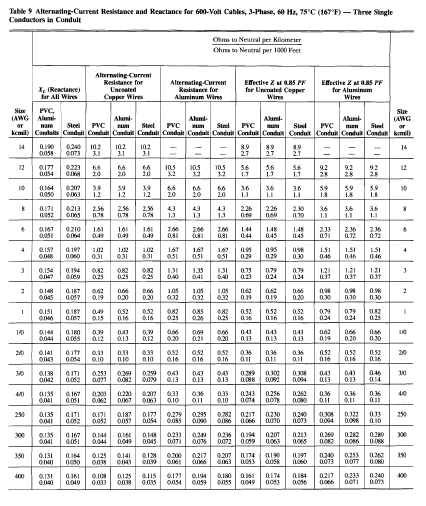
Example: Double Line to Ground Fault Calculation

Read
Double Line to Ground Fault

Double line to ground fault when both phases on the three phase line are accidentally connected to the ground. In this case, fault current will flow from the line to the ground within the involved phases, say, Phase B and Phase C.

Example:

From the figure given below, assume that the generator is solidly grounded and neglect the fault impedance. Determine the phase currents and phase voltage when Line to Line fault occurs in the system.



The article Unbalanced Fault Analysis: Double Line to Ground Fault explained and derived that all sequence network are connected in parallel to satisfy the conditions in this type of fault.

Thus,

Equivalent Sequence Network of DLG Fault


By circuit analysis we can get the equivalent impedance as,

  • Zeq = Z1//Z2 + Z0 = j0.1//j0.1 + j0.25 = j0.3 pu
Let the value of Ea = 1 (angle 0). 

Therefore, the value of the +s current is, 
  • Ia1 = Ea / j0.3 pu = -j 3.33 pu

By current division, we can say that the respective values of -s and 0s current as,
  • Ia2 = Ia0 = - (-j 3.33/2) = j 1.67 pu
Summary of sequence currents, 
  • Ia1 = -j 3.33 pu
  • Ia2 = j 1.67 pu
  • Ia0 = j 1.67 pu
  • Fault Current at Phase A, IA = 0.
  • Fault Current at Phase B, IB = 5 (angle -30) pu
  • Fault Current at Phase C, IC = 5 (angle -150) pu
Apply base values, 
  • Choose: Sb = 20 MVA and kVb = 13.8 kV, then... 
  • Ea = 20 MVA/ 20 MVA = 1 (angle 0) per unit.
  • Ibase = 20 MVA / (1.73 x 13.8 kV)
  • Ibase = 0.837 kA

Therefore the actual Fault Current Values are, 
  • IA = 0
  • IB = 5 x 0.837 kA = 4.185 kA (angle -30) 
  • IC = 5 x 0.837 kA = 4.185 kA (angle -150) 
Voltage Values,

Based on the equivalent sequence network,

  • Va2 = Z2 x Ia2 = j 0.1 x (-j 1.67) = 0.167 (angle 0) pu
  • Therefore it follows that,  Va2 = Va0 = 0.167 (angle 0) pu
  • VA = 0.501 (angle 0) pu
  • VB = VC = 0
Apply voltage base, 
  • VA = 0.501 x (13.8 kV/1.73) = 3.996 kV
  • VB = VC = 0
Tags :
Created By Themexpose