What is symmetrical components?

The method of symmetrical components is used to analyze unbalance system by converting it to three sets of balanced phasors.

Supposed there is an unbalanced three phase current of Ia, Ib and Ic. These values can be represented by its corresponding symmetrical components such as the following:

• positive sequence: I1
• negative sequence: I2
• zero sequence: I0

To find the values of the above components, the following matrix formula will be used.

Phase Values to Sequence Components

where:

α = 1 ë 120 degrees.

From the above formula we can get, 

I0 = 1/3 (IA + IB + IC)

I1 = 1/3 (IA + IB*a + IC*a*a)

I2 = 1/3 (IA + IB*a*a + IC*a)

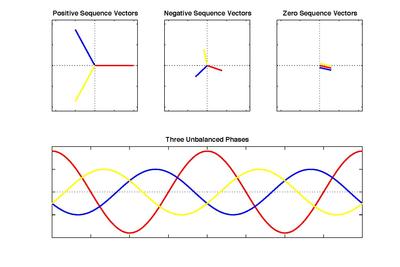
In this diagram, the unbalanced phasors are broken down into balanced phasors. As seen from diagram above, Va1 (positive sequence) rotates counter-clockwise with a sequence of Va1, Vb1 and Vc1, these vectors are of equal magnitude and 120 degrees apart. 

In the same situation, Va2 (negative sequence) also rotates counter- clockwise with a sequence f Va2, Vc2 and Vb2. Negative sequence vectors have also equal magnitude and 120 degrees apart. 

Here, the difference between the positive sequence and negative sequence can be distinguished by looking at the sequence and order of vector rotation. 

Lastly, Va0 (zero sequence) have vectors of equal magnitude but these vectors are in-phase with each other. Meaning there is no angle of displacement between vectors. 

Similarly, given symmetrical components values, it can be converted back to phase values using the following matrix formula:

Sequence components to Phase Values Matrix

Example: 
The electrical system has three unbalanced current of Ia = 100 ë50 A; Ib = 75 ë35 A; Ic= 65 ë45. Find the corresponding symmetrical component values?
From the formula given above,
I0 =  1/3 (Ia + Ib + Ic)
I1 = 1/3 (Ia + Ib * α + Ic * α * α)
I2 = 1/3 (Ia + Ib * α * α + Ic * α )
note: α = 1 ë 120 degrees.

 Calculating values, the results are:

I0 = 80 ë44 A.
I1= 16 ë74 A
I2= 7 ë 77 A.

The symmetrical components are very important in calculating fault analysis. This is because all parts of electrical power system such as motors, generators, transformers and transmission lines can be represented by its corresponding sequence network components.